【データ可視化入門】データ活用において見るべき数値について

この記事について

この記事は【データ可視化入門】と題しており、データアナリストの業務の基本やポイントを説明していきます。データの分析と可視化がなぜ必要かを考えることから始め、見るべき数値となる集計値、実務のイメージ、気をつけたいことまでを押さえていきます。

対象ユーザ	・データ分析業務の初心者・これからデータアナリストを目指す人
内容	・ビジネスのためのデータ活用イメージ・よく利用される指標（平均値/中央値/標準偏差）・グルーピング・気をつけたいこと
注意点	可視化作業やレポーティング業務の基本となる考え方を解説します。SQLのテクニックやBIツールの使い方を取り上げるものではありません。

何のためにデータの可視化をするの？

まずは、そもそも何のためにデータを分析し可視化するのか（＝何のためにデータアナリストという役割が必要とされているのか）を考えてみましょう。

大原則は非常にシンプルです。それは、 “ビジネスの成長にデータを役立てる” です。

現在置かれている状況や事業の傾向を確認することで、根拠を持った意思決定を行い、有効な施策の実行に繋げることが可能です。

ただ、データを利用するといってもそのままの状態ではまともな判断はできません。ちょっとした規模のデータでも人間の認知能力を軽く超えてきます。

たとえば、ECサイトで健康食品を販売している会社の経営者に向かって「●月●日の●時●分にアクセスしたAさんは商品コードxx-xxxxのものを購入し●●県に発送指示がありました。次にBさんは商品コードxx-yyyyのものを購入し▼▼県に…、つづいてCさんは…」というように報告していったらどうでしょうか。長時間説明しても「結局、関東のお客さん向けのサプリメント半額キャンペーンは成功したの？」といったリアクションになるでしょう。このようなビジネスの意思決定に関する問いに答えるためには、生の購入データを見るのではなく、それらをベースにした解釈をする必要があります。

したがって、集計値 で解釈のとっかかりを準備する必要があります。そして、その値をグラフなどで上手に（かつ適切に）可視化することで、施策のジャッジや意思決定をしていくことが可能です。

まずは見るべき数値としての集計値を説明します。集計値といっても難しくありません。よく聞くのは、合計 / 件数 / 平均値 / 最頻値 / 中央値 / 標準偏差などでしょう。端的に言うと、データ全体に関するデータと言えます。

集計値について解説

ごく一部ですがデータアナリストであれば必須の集計値の知識を解説します。

1. 合計 SUM

合計は言葉のとおり、足し算をした結果のことです。

3人家族のAさんがこの1ヶ月間で利用した生活費はおよそ25万円で、計算の仕方は
家賃＋食費＋日用品費＋光熱費＋通信費＋交通費＋娯楽費＋書籍代というイメージです。

細かい詳細は不要だが全体の規模を知りたい、というときに利用します。再来年●●万円のマンションを買いたいがどのくらいローンで借りることになるのか、ということを考える場合、食費にいくら使っているかは重要ではなく、全体でいくら消費しているかを知りそこから貯金額を考えるのです。

2. 件数 COUNT

件数も言葉のとおりで、数え上げた結果のことです。

例1：私は先月10回外食をした。
例2：最近3ヶ月間で社員Aがとってきた契約は30件だった。

合計が重要なのか件数が重要なのかは場面によります。例2の社員Aさんがとった30個の契約の合計売上が400万円である場合、もしもこの会社が売上目標に重きを置いていたり資金繰りが厳しかったりしたら合計売上が指標として利用されると思いますが、顧客層を厚くして口コミを広げてもらうことを戦略上重視していれば件数が使われるというイメージです。

3. 平均値（期待値） AVERAGE

平均値は一番無難な集計指標でしょう。件数が多いから合計が多い、というような影響を排除して比較ができるためよく利用されます。全体をならしたときの値という意味のため、割り算を使います。

先月の自社製サプリメントの売り上げが500万円で購入者が5,000人だったとき、購入者の平均利用金額は 500万円÷5,000＝1,000円となります。

平均値は、そのグループに関しておおざっぱなイメージをわかりやすく与えてくれます。購入金額の平均が1,000円の自社製サプリメントと、400円の他社製サプリメントを比べた場合、自社製であれば高くても買われやすい傾向にあると判断できますので、今後の値段設定にも利用できます。

4. 中央値 MEDIAN

中央値は、順位づけしたときにちょうど真ん中にくる値のことです。平均値と同じで、その集団の大体の傾向を教えてくれます。割り算するだけで済む平均値と違い、順位どおりに並び替えて上から数え上げるという作業が発生するので人間が出すのはなかなか大変です（数が増えてくると機械に任せる必要があります）。

自社製サプリメントの購入者5,000人を購入金額でランキングをつけ、2,500位の人の金額が750円の場合は中央値は750円です（正確に言うと2,501位の人も真ん中の順位なのでどちらを使うか迷ってしまいますが、大きな問題になりません）。

中央値の特徴は、外れ値（＝イレギュラー）の影響を受けづらいことです。ここが平均値と大きく違います。たとえば、購入金額1位の人が350万円で、残り4,999人の合計が150万円という場合を考えてみましょう。

この場合、このサプリメントはたまたま一人の業者と思われるお客さんのおかげで500万円の売り上げを達成していますが、大多数の人は全然お金を払っていないということになります。今回500万円の売上を達成しているのはラッキーでした。

このような危機的状況でも、平均値を使うと一人当たりの購入金額が1,000円ということになり、状況を見誤ります。つまり、平均値は極端な外れ値の影響をしっかりうけてしまうのです。中央値であれば、今回の場合おそらく300円くらいになるでしょうから、この会社の自社製サプリメントは全然売れておらずリニューアルする必要がある、という正しい判断に行き着きます。

5. 標準偏差（と分散） STANDARD DEVIATION (VARIANCE)

どれだけ全体の数値がバラついているのかを表現することができる指標です。

全員が1,000円購入している場合、購入金額の標準偏差や分散はゼロです。反対に小さい金額と大きい金額が入り乱れている場合大きくなります。

これらは単体で利用するというより、平均値や中央値と組み合わせて使うことで実態に寄り添った分析をサポートしてくれます。

集計値のグルーピングの考え方

集計値の意味について確認しましたが、これらは集団についての情報であるためグルーピングの考え方が不可欠です。グルーピングの基準や粒度（＝大雑把さや細かさ）を考えて、適切に設定してあげることがデータ分析には必要です。

グルーピングの方法1：顧客の性質（属性）に注目する

たとえば、男女で分ける方法があります。男女差が如実に現れる商品のマーケティングなどではこれは定番でしょう。
マーケティング以外でも、たとえば営業係の営業成績を分析し、成約率向上につなげる場合を考えてみましょう。まずは横軸にアポイント件数、縦軸に成約件数をとって可視化してみます。ちなみにこれは散布図といいます。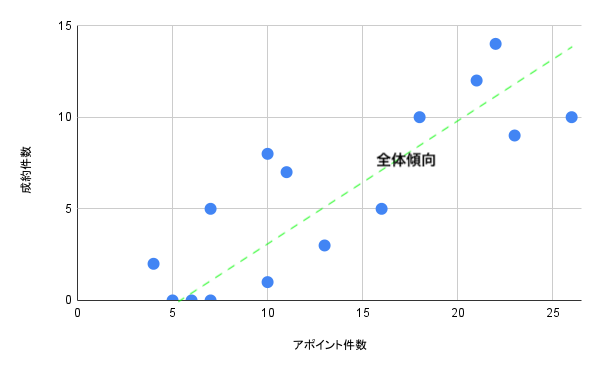

なんとなくアポイント件数が増えると成約も増えそうですが、少しデータが散らばっていますね。トレンドを表す直線からかなり離れている点がいくつもあり、すこし強引な結論にも感じられます。

ですが、もし男女別に色分けして次のような散布図が得られたらどうでしょうか。先ほどのトレンドを表す直線より収まりが圧倒的に良く、より傾向が顕著に浮かび上がってきます。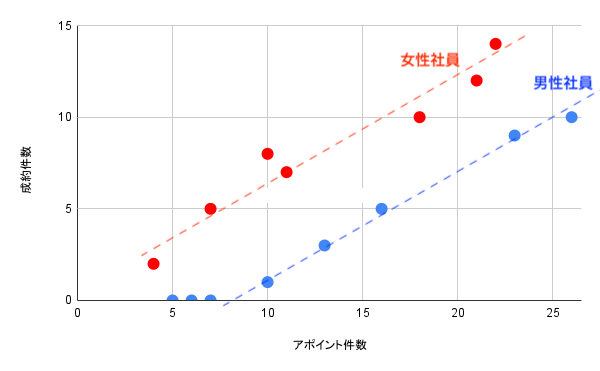

こう見てみると、成約にはなにはともあれアポイントが重要と言ってよさそうです。ついでに、男性社員より女性社員の方がかなり有利であるということもわかりました（ほかにも、出身地エリアや年代、新卒入社か中途入社かといったグルーピングが有効だった可能性もありますね）。

グルーピングの方法2：時系列に注目する

経営状況を表す場合などをはじめとして、時間の変化とともにどのように指標が変化したかを追うことは非常に重要です。

年月や日付ごとに代表した値をプロットしグラフでつなぐと、その時期における傾向がよくわかります。以下の図は、日付ごとにアメリカの金利とナスダック指数を集計し折れ線グラフで可視化したものです（集計値としては、ファイナンス分野に特有な終値といわれるものを採用しています）。株価の成長具合と、ついでに金利との相関関係がしっかりと伝わると思います。

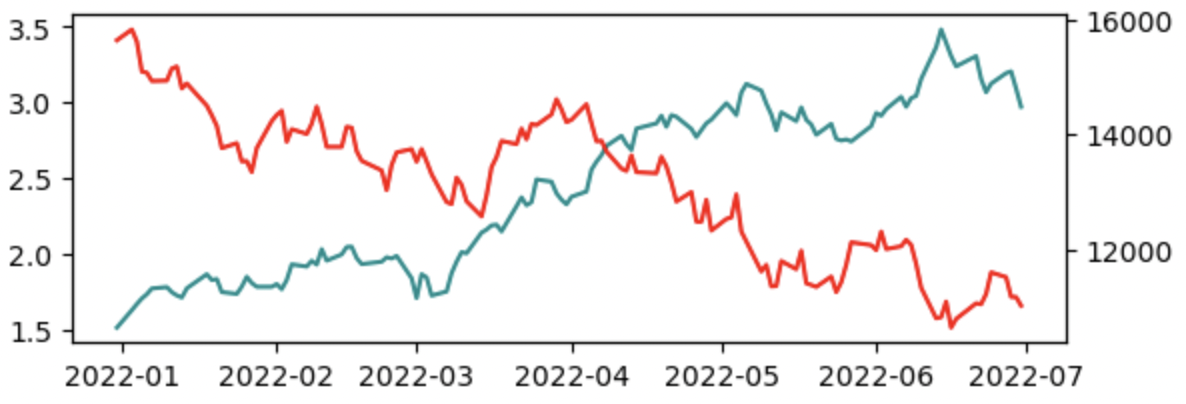
分析対象によっては、週次や月次で集計したり年次で集計したりすることが有効な場合もあり、どの粒度にするかの判断が重要なところです。

可視化の考え方

適切なグルーピングで、データに関するデータである集計値を計算したら、あとは可視化をしていきましょう。

集計値は生のデータを単純化してくれています。それが可視化というプロセスを経ることで、さらに理解しやすい情報に加工することができます。無造作に羅列された数字は、理解するだけでも負担がかかります。そんな状態で大事なビジネスのジャッジをするのは得策ではありません。データアナリストは、一目で要点が伝わるレポートを作らなくてはなりません。

可視化の手段やポイントはいくつも存在し、伝えたい意図（メッセージ）も踏まえてよく考える必要がありますが、それは別の記事にてお伝えできればと思います。

気をつけたいこと

集計値の使い方とグループ分け、可視化のイメージをざっくり把握できたところで、ぜひ覚えておいてほしいことがあります。これから良くない分析の例を示します。このような分析を皆さんは行わないように気をつけてください。

失敗1：分析範囲が不適切

データは客観的なものと誰もが信じていると思いますが、見せ方によっては “嘘をつかせる” こともできます。たとえば、誘導したい結果に反するデータを“なかったこと”として扱うことができます（都合の悪いことは報告しなければよいのです）。

先ほど株価が成長していることを示した分析でも、2022年5月から1か月程度だけを集計してグラフ化したらどうなるでしょうか。グレーのエリアを横方向に引き伸ばして見せれば、緑のラインが緩やかに下がっていることを示せるので、誰もがアメリカの株価が衰退していると考えるはずです（さっきとは真逆の結論になります）。

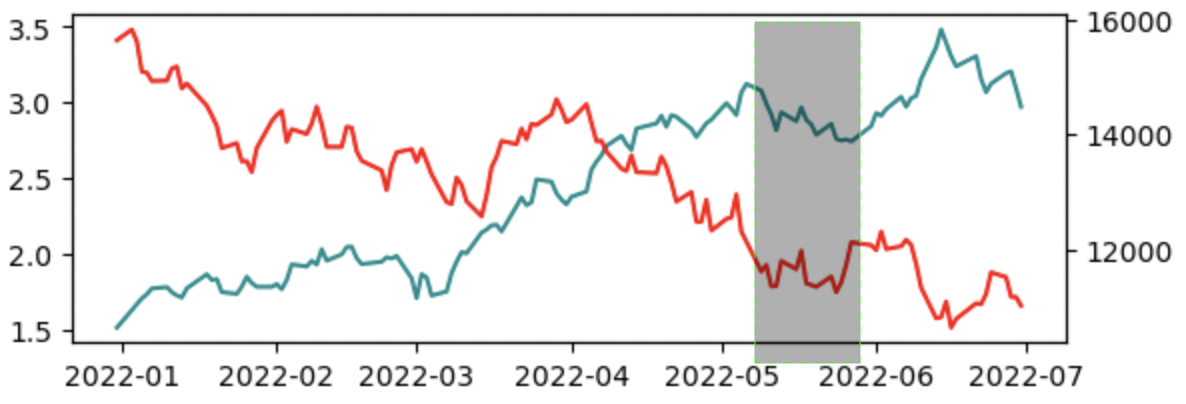
気をつけなくてはいけないのは、これは意図的に実現できることではありますが、意図せず陥ってしまうことがあるということです。私が最初にみせたグラフの期間の方こそ誤っているという主張もありうるでしょう。どちらが妥当なのかはしっかりと吟味する必要があり、場合によっては自分だけで判断せずチームや会社規模での合意を取り付けておくべきです。

失敗2：グルーピングが適切でない

男女でグルーピングすることでデータがすっきりする場合があります。上述の営業成績の例などが顕著でしょう。

お客さんを年代でわけることも有効でしょう。ただ、どのような粒度で分けるかが重要です。10代/20代/30代/…と細かく分けて集計してよくわからない場合、学生/社会人/シニアのようにある程度大雑把に分けることで意味のある分析になる可能性があります。

意味のあるグループ分けには理由がある場合も多いです。そのグループ分けがなぜうまくいって、別のグループ分けがなぜうまくいかないのかを考えてみる癖をつけましょう。

失敗3：平均値の使い方を誤っている

平均値は簡単な計算で出すことができるのでわかりやすく使いやすいですが、意味のない平均や誤った平均というものが存在します。たとえば、以下の二つのパターンがあり、このようなミスはデータアナリストとして絶対にしてはいけません（もしかしたら小学生の頃に習ったことがあるかもしれません）。

＜パターン1＞男子生徒の平均身長が165cmで女子生徒の平均身長が155cmのとき、男女比を考えることなく生徒全体の平均身長を160cmとしてしまう。

男子生徒が女子生徒より多い場合、生徒全体の平均身長は160cmより高くなり165cmに近づきます。
正しく計算する場合は加重平均という考え方が必要です。男子の人数が多く165cmの影響力が大きいので、そちらに重みをつける必要があるということです。

＜パターン2＞行きは時速5kmで歩き、帰りは時速15kmを維持して走った際の往復の平均時速を10kmとしてしまう。

正しくはそれより遅い時速7.5kmです。せっかく早いスピードで走っても、その分すぐ走り終わってしまい、あまり全体へ影響を与えられないからです。
調和平均という考え方が必要です。

失敗4：施策実現が困難な要素があり、データ分析が数字遊びになっている

あるベテランアスリートの記録を伸ばしたいという目的があったとします。近年におけるその人の各試合の記録と、大会準備期間中の練習量/睡眠量/摂取した栄養素などの関係性を分析することは非常に有効です。ですが、分析スコープを拡大して年齢と記録の関係性を調べてしまうことはどうでしょうか。

年齢が若いほど記録がよいという結論が得られる可能性は大いにあります。しかし、それがわかったところでどうなるのか。そのアスリートは若返ることはできません。この人物の記録を伸ばしたい、という目的がある以上このような分析はほとんど役に立たないでしょう。何のために分析を行うのか、という目的はストイックなほどに常に意識してください。

失敗5：データの定義が複雑で解釈が困難

集計作業とうまく付き合っていくことがデータアナリストの鉄則ですが、なにも平均値や中央値だけと仲良くする必要はありません。オリジナルの指標をつくっても問題ありません。複雑な計算ロジックを組むのも大丈夫です。

各国の生産年齢人口をGDPで割った値の3乗の自然対数を集計し、国別ランキングをつくってもよいでしょう。

log(生産年齢人口 / GDP ) ^3

この不思議な値は、一人当たりが貢献しているGDP、すなわち生産性と逆の増減をします。生産性が高い国ではこの値は低いですし、生産性が低い国ではこの値が高くなります。

ですが、それならシンプルに GDPを生産年齢人口で割った生産性を集計値としたほうがよいと思います。複雑な処理（このケースでは、あえて逆数をとって3乗したりlogをとったりすること）をすると分析の正確性が高まることがありますが、生産性の高い国に投資するときのリターンを考えるときなどに、この集計値の複雑さは役に立ちません。複雑な計算処理をすることで少しズレていたトレンドの直線がぴったりかさなるようになったとしても、それはビジネスにおいて重要なことではなく、上述した数字遊びに近いです。

いずれ施策の決定権を持つ企画担当や役員に理解してもらえるように説明する必要がでてくるという観点からも、シンプルな方がビジネス上は何倍も都合がよいと言えます。※1

また、集計は継続的に実施して意味がでてきます。無駄な計算負荷をかけることや、後任のデータアナリストが理解できないロジックを使うことは問題になります。

※1.回帰分析という統計手法があります。先ほどの「アポイント件数と成約件数の散布図」に直線を引くという操作のことですが、なぜここでは放物線である2次関数や、ぐにゃぐにゃした3次関数を描かず、あえて1次関数を選択するのでしょうか（理論上、次数が大きければ大きいほどどんな形のトレンド線も再現できるというのに）。大きく分けて二つあります。

一つは、傾向がわかれば十分という場面では、単純な直線が一番利用しやすいから。

もう一つは、〇〇件アポイントをとれば▼▼件成約する、というようなわかりやすい知見をビジネスに登用することができるからです。1次関数でない場合、変化の割合（＝接線の傾き・微分係数）が一定ではないので、このようなことはできません。

どちらの理由も、少しくらい誤差が出てしまってもビジネス的にはシンプルな方がマシ、ということですね。